DCGAN

Generative Adversarial Networks (GAN)

Generative modeling is an unsupervised learning task in machine learning that involves automatically discovering and learning the patterns in input data in such a way that the model can be used to generate or output new examples that plausibly could have been drawn from the original dataset.

A generative adversarial network (GAN) has two parts:

The generator learns to generate plausible data. The generated instances become negative training examples for the discriminator.
The discriminator learns to distinguish the generator's fake data from real data. The discriminator penalizes the generator for producing implausible results.

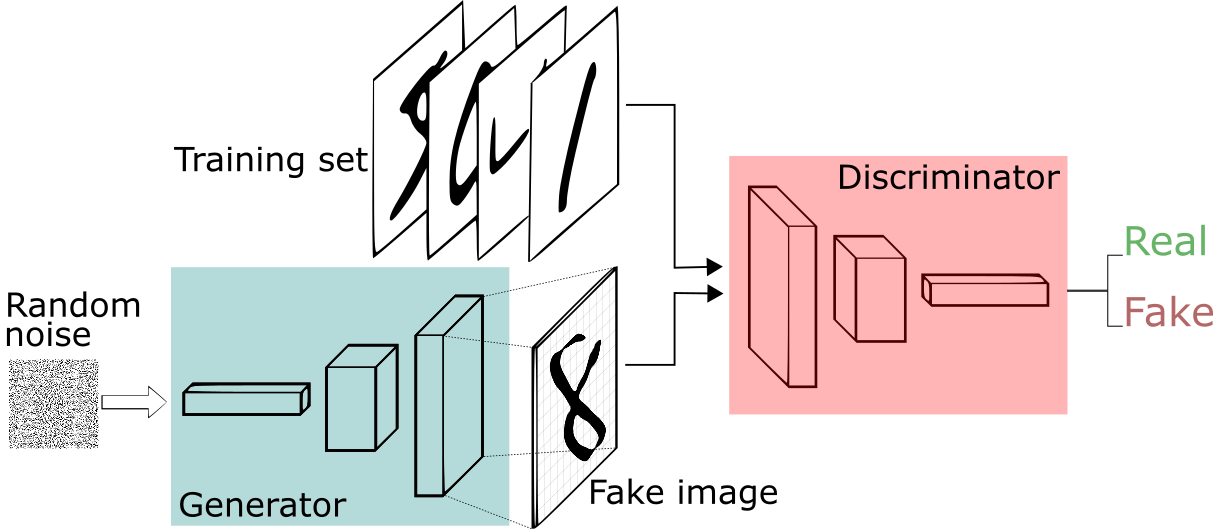
Both the generator and the discriminator are neural networks. The generator output is connected directly to the discriminator input. Through backpropagation, the discriminator's classification provides a signal that the generator uses to update its weights.

Deep Convolutional GAN (DCGAN)

DCGAN, or Deep Convolutional GAN, is a generative adversarial network architecture that uses convolution layers (Discriminator) and transposed convolution layers (Generator). Batch Normalization is used in both, the Generator and Discriminator except for the final layer. ReLU activation is used in the generator for all layers except for the output layer, which uses Tanh activation. LeakyReLU activation is used in the discriminator for all layers.

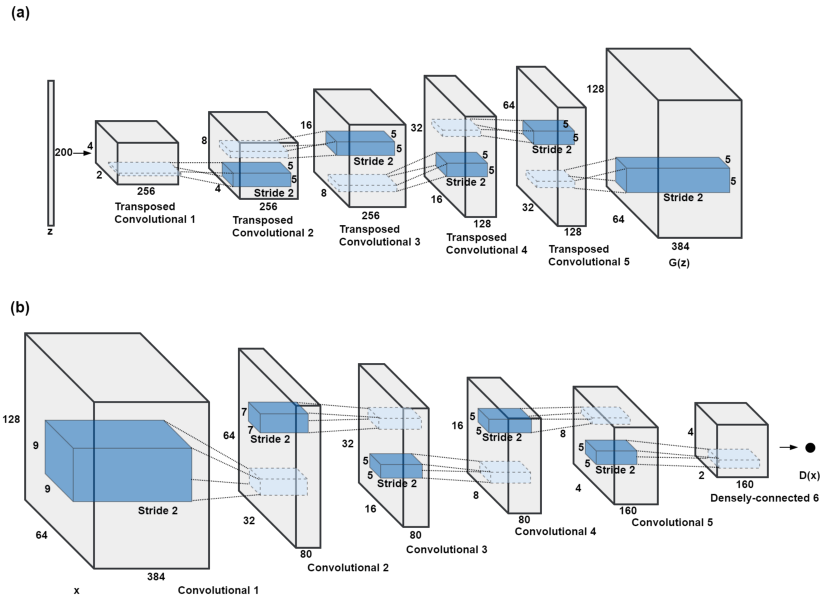
Training a DCGAN on MNIST Dataset

We will start by importing the libraries that will be required to train our DCGAN model. We will be using PyTorch for building our model.

import torch
from torch import nn
from tqdm.auto import tqdm
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid 
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

Generator

Now let us start by creating the Generator that will generate our images.

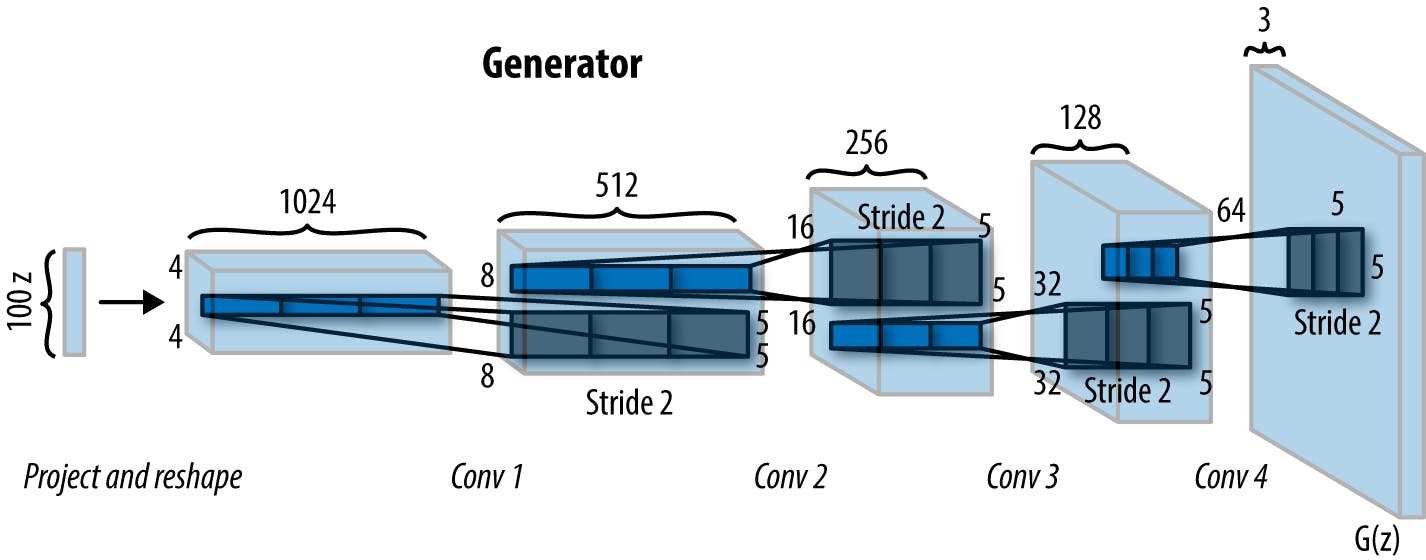
Our generator class will take the dimension of the noise matrix, the number of channels in the images (default = 1), as we are using grayscale images, and the number of nodes in the first hidden layer (default = 64) for initialization.

The instance of our Generator will take noise as its input.

class Generator(nn.Module):
    '''
    Generator Class

    Parameters:
        z_dim: Dimension of the noise vector, a scalar
        im_channels: Number of channels in the generated image (default: 1), a scalar
        hidden_dim: The inner dimension, a scalar
    '''

    def __init__(self, z_dim=10, im_channels=1, hidden_dim=64):
        '''
        Create a Generator
        '''
        super(Generator, self).__init__()
        self.gen = nn.Sequential(
            self.make_gen_block(z_dim, hidden_dim*4),
            self.make_gen_block(hidden_dim*4, hidden_dim*2, kernel_size=4, stride=1),
            self.make_gen_block(hidden_dim*2, hidden_dim, kernel_size=3, stride=2),
            self.make_gen_block(hidden_dim, im_channels, kernel_size=2, stride=2, final_layer=True)
        )

    def make_gen_block(self, input_channels, output_channels, kernel_size=3, stride=2, final_layer=False):
        '''
        Create a sequence of operations corresponding to a Generator block of DCGAN.
        Sequence of a transposed convolution, a batchnorm (except for in the last layer), and an activation.

        Parameters:
            input_channels: Number of channels in the input feature representation.
            output_channels: Number of channels in the output feature representation.
            kernel_size: The size of each convolutional filter (default=3).
            stride: The stride of the convolution (default=2).
            final_layer: Keep Track of the final layer, a boolean (default=False).
        '''
        if final_layer:
            return nn.Sequential(
                nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
                nn.Tanh()
            )

        else:
            return nn.Sequential(
                nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
                nn.BatchNorm2d(output_channels),
                nn.ReLU(inplace=True)
            )

    def forward(self, noise):
        '''
        Function for completing a forward pass of the generator: Given a noise tensor, 
        returns generated images.

        Parameters:
            noise: a noise tensor with dimensions (n_samples, z_dim)
        '''
        return self.gen(noise)

Each block of our generator consists of a transposed convolutional layer (ConvTranspose2d) and a batch normalization layer (BatchNorm2d) followed by a ReLU activation except for the output layer, which uses a Tanh activation.

Discriminator

Now let us create the generator that will distinguish between the fake images generated by our generator and the real images from the MNIST dataset.

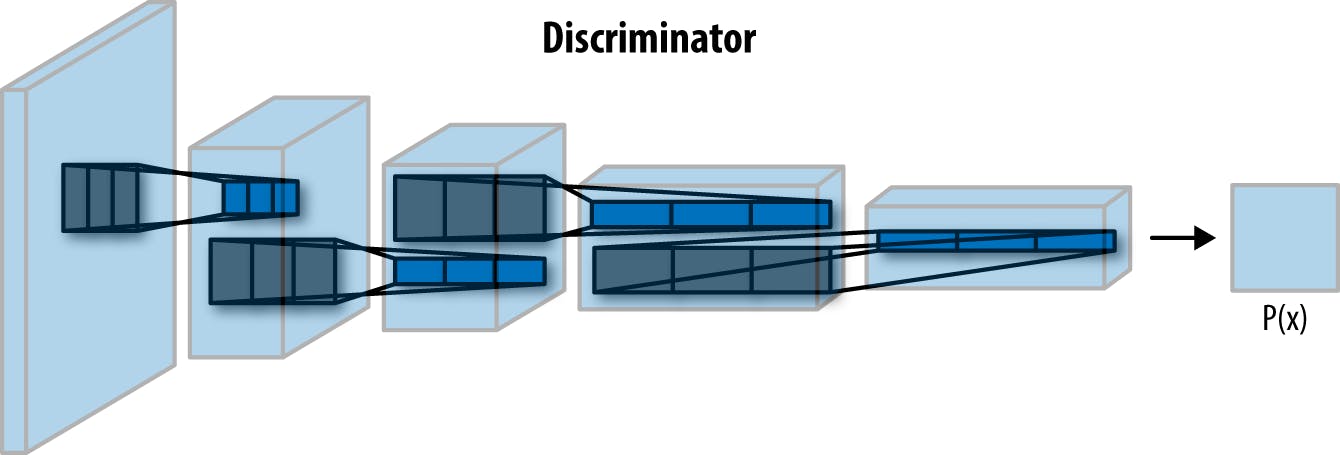
Our discriminator will take the image as the input and will output whether the image is real or fake.

class Discriminator(nn.Module):
    '''
    Discriminator class

    Parameters:
        im_channels: Number of channels in the input image, a scalar
        hidden_dim: The inner dimension, a scalar
    '''
    def __init__(self, im_channels=1, hidden_dim=16):
        '''
        Create a Discriminator
        '''
        super(Discriminator, self).__init__()

        self.disc = nn.Sequential(
            self.make_disc_block(im_channels, hidden_dim),
            self.make_disc_block(hidden_dim, hidden_dim*2),
            self.make_disc_block(hidden_dim*2, 1, final_layer=True)
        )

    def make_disc_block(self, input_channels, output_channels, kernel_size=4, stride=2, final_layer=False):
        '''
        Create a sequence of operations corresponding to a Discriminator block of DCGAN.
        Sequence of a convolution, a batchnorm (except for in the last layer), and an activation.

        Parameters:
            input_channels: Number of channels in the input feature representation.
            output_channels: Number of channels in the output feature representation.
            kernel_size: The size of each convolutional filter (default=3).
            stride: The stride of the convolution (default=2).
            final_layer: Keep Track of the final layer, a boolean (default=False).
        '''
        if final_layer:
            return nn.Sequential(
                nn.Conv2d(input_channels, output_channels, kernel_size, stride)
            )
        else:
            return nn.Sequential(
                nn.Conv2d(input_channels, output_channels, kernel_size, stride),
                nn.BatchNorm2d(output_channels),
                nn.LeakyReLU(negative_slope=0.2, inplace=True)
            )

    def forward(self, image):
        return self.disc(image).view(len(image), -1)

Noise

Now that we have our generator and discriminator, let us start creating noise to be used in our training.

def generate_noise(n_samples=100, z_dim=10, device="cpu"):
    '''
    Generate a noise tensor of shape (n_samples, z_dim, 1, 1)

    Parameters:
        n_sample: Number of samples in noise tensor, a scalar.
        z_dim: Dimension of noise vector, a scalar.
    '''
    noise = torch.randn(n_samples, z_dim).to(device)
    return noise.view(len(noise), z_dim, 1, 1) #width=1, height=1, n_channels=n_dim

Training

For our training, we will need to load our dataset and define the following parameters:

criterion: the loss function
n_epochs: the number of times you iterate through the entire dataset when training
z_dim: the dimension of the noise vector
display step: how often to display/visualize the images
batch size: the number of images per forward/backward pass
learning rate: the learning rate
beta_1, beta_2: the momentum term
device: the device type

So let us define them and load the MNIST dataset to be used for training,

criterion = nn.BCEWithLogitsLoss()
n_epochs = 100
z_dim = 64
display_step = 500
batch_size = 128
lr = 0.0002
beta_1, beta_2 = 0.5, 0.999
device = "cuda"

#Transforms to apply to our dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

#Load the MNIST dataset
dataloader = DataLoader(
    MNIST('.', download=False, transform=transform),
    batch_size=batch_size,
    shuffle=False
)

Now, we will have to create instances of our Generator and Discriminator classes and define optimizers for them respectively,

gen = Generator(z_dim).to(device)
gen_opt = torch.optim.Adam(gen.parameters(), lr=lr, betas=(beta_1, beta_2))
disc = Discriminator().to(device) 
disc_opt = torch.optim.Adam(disc.parameters(), lr=lr, betas=(beta_1, beta_2))

Here, we are using Adam optimizer.

Now, we initialize the weights to the normal distribution with mean = 0 and standard deviation = 0.02.

def weights_init(m):
    if isinstance(m, nn.Conv2d) or isinstance(m, nn.ConvTranspose2d):
        torch.nn.init.normal_(m.weight, 0.0, 0.02)
    if isinstance(m, nn.BatchNorm2d):
        torch.nn.init.normal_(m.weight, 0.0, 0.02)
        torch.nn.init.constant_(m.bias, 0)

gen = gen.apply(weights_init)
disc = disc.apply(weights_init)

We would also need a function to help us visualize our training process. Hence we will now create a function for the same.

def show_tensor_images(image_tensor, num_images=25, size=(1, 28, 28)):
    '''
    Function for visualizing images: Given a tensor of images, number of images, and
    size per image, plots and prints the images in an uniform grid.
    '''
    image_tensor = (image_tensor + 1) / 2
    image_unflat = image_tensor.detach().cpu()
    image_grid = make_grid(image_unflat[:num_images], nrow=5)
    plt.imshow(image_grid.permute(1, 2, 0).squeeze())
    plt.show()

Finally!!!!

Putting it all together!

n_epochs = 50
cur_step = 0
mean_generator_loss = 0
mean_discriminator_loss = 0
for epoch in range(n_epochs):
    # Dataloader returns the batches
    for real, _ in tqdm(dataloader):
        cur_batch_size = len(real)
        real = real.to(device)

        ## Update discriminator ##
        disc_opt.zero_grad()
        fake_noise = generate_noise(cur_batch_size, z_dim, device=device)
        fake = gen(fake_noise)
        disc_fake_pred = disc(fake.detach())
        disc_fake_loss = criterion(disc_fake_pred, torch.zeros_like(disc_fake_pred))
        disc_real_pred = disc(real)
        disc_real_loss = criterion(disc_real_pred, torch.ones_like(disc_real_pred))
        disc_loss = (disc_fake_loss + disc_real_loss) / 2

        # Keep track of the average discriminator loss
        mean_discriminator_loss += disc_loss.item() / display_step
        # Update gradients
        disc_loss.backward(retain_graph=True)
        # Update optimizer
        disc_opt.step()

        ## Update generator ##
        gen_opt.zero_grad()
        fake_noise_2 = generate_noise(cur_batch_size, z_dim, device=device)
        fake_2 = gen(fake_noise_2)
        disc_fake_pred = disc(fake_2)
        gen_loss = criterion(disc_fake_pred, torch.ones_like(disc_fake_pred))
        gen_loss.backward()
        gen_opt.step()

        # Keep track of the average generator loss
        mean_generator_loss += gen_loss.item() / display_step

        ## Visualization code ##
        if cur_step % display_step == 0 and cur_step > 0:
            print(f"Epoch {epoch}, step {cur_step}: Generator loss: {mean_generator_loss}, discriminator loss: {mean_discriminator_loss}")
            show_tensor_images(fake)
            show_tensor_images(real)
            mean_generator_loss = 0
            mean_discriminator_loss = 0
        cur_step += 1

Results

Here's roughly the progression you should be expecting. On GPU this takes about 30 seconds per thousand steps. On the CPU, this can take about 8 hours per thousand steps.

You can find the code for this blog here.

Deep Convolutional GAN (DCGAN)

Table of contents

Generative Adversarial Networks (GAN)

Deep Convolutional GAN (DCGAN)

Training a DCGAN on MNIST Dataset

Generator

Discriminator

Noise

Training

Results